دانلود رایگان پروژه الگوریتم بهینه سازی عنکبوت اجتماعی SSA – SSO با MATLAB
در این پست دانلود رایگان پروژه الگوریتم بهینه سازی عنکبوت اجتماعی SSA با متلب را به همراه مقاله و پاورپوینت آماده کرده ایم که امیدواریم مورد استفاده شما عزیز قرار گیرد.
الگوریتم بهینه سازی عنکبوت اجتماعی یا SSA – Social Spider Algorithm یا SSO یک الگوریتم بهینه سازی نوین است که در سال 2015 توسط شخصی به نام جیمیز ارائه شده است. در طی سال های متعدی، عنکبوت در هوش مصنوعی، موضوع تحقیقاتی بسیاری از پژوهشگران در مقایسه با دیگر حیوانات بوده است. می توان رفتار جستجوگر عنکبوت اجتماعی را، حرکت همگانی آنها به سوی منبع غذایی عنوان کرد.
در وب، عنکبوت ارتعاشات منتشر شده را به منظور مشخص کردن مسیر بالقوه منبع غذایی، دریافت و تحلیل می نماید. به جهت بهینه سازی در فضای جستجو به روش SSO یا SSA ، این رفتار طبیعی مورد استفاده قرار می گیرد. فضای جستجو مسئله بهینه سازی در SSA ، وب چند بعدی عنکبوت در نظر گرفته می شود.
توضیحات بیشتر، فیلم، تصاویر خروجی و لینک دانلود رایگان پروژه الگوریتم بهینه سازی عنکبوت اجتماعی SSA با متلب در ادامه مطلب.
هر یک از موقعیت ها در وب، نشان از این می باشد که برای مسله بهینه سازی، یک راه حل عملی است. همینطور، عمل وب به منزله رسانه انتقال ارتعاشات تولید شده به وسیله عنکبوت می باشد. در وب، هر عنکبوت یک موقعیت و یک برازش دارد و نشان دهنده پیدا کردن منبع غذایی در آن موقعیت است. عنکبوت قارد به حرکت در وب به صورت آزاد است اما قادر به تک وب نمی باشد.
زمانی که یک عنکبوت بخواهد به طرف یک موقعیت جدید حرکت کند، از حرک خود ارتعاشی تولید خواهد شد که در کل وب انتشار پیدا می کند. هر یک لرزش های عنکبوت، شامل اطلاعاتی از یک عنکبوت می باشد و دیگران نیز می توانند این اطلاعات ارتعاش را دریافت کنند.
قسمتی از کدهای پروژه الگوریتم بهینه سازی عنکبوت اجتماعی با متلب :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 | function result = main(func, dim, bound, max_iter, pop_size, r_a, p_c, p_m, info) if (nargin == 0) func = @(x)sum(x.^2, 2); dim = 30; bound = 100; max_iter = 10000; pop_size = 25; r_a = 1; p_c = 0.7; p_m = 0.1; info = true; end g_best = Inf; g_best_hist = []; g_best_pos = zeros(1, dim); position = rand(pop_size, dim) * 2 * bound - bound; target_position = position; target_intensity = zeros(pop_size, 1); mask = zeros(pop_size, dim); movement = zeros(pop_size, dim); inactive = zeros(pop_size, 1); if (info) fprintf(' SSA starts at %sn', datestr(now)); fprintf('==============================================n'); fprintf(' iter optimum pop_min base_dist mean_dist time_elapsedn'); fprintf('==============================================n'); start_time = java.lang.System.currentTimeMillis; end iter = 0; while (iter < max_iter) iter = iter + 1; spider_fitness = func(position); base_distance = mean(std(position)); distance = squareform(pdist(position)); if (min(spider_fitness) < g_best) [g_best, ind] = min(spider_fitness); g_best_pos = position(ind, :); end g_best_hist = [g_best_hist g_best]; if (info && (iter == 1 || iter == 10 ... || (iter < 1001 && mod(iter, 100) == 0) ... || (iter < 10001 && mod(iter, 1000) == 0) ... || (iter < 100000 && mod(iter, 1000) == 0))) elapsed_time = java.lang.System.currentTimeMillis - start_time; fprintf(['% 5s %.4e %.4e %.4e %.4e %02d:%02d:%02d.%03dn'], num2str(iter), ... g_best, min(spider_fitness), base_distance, mean(mean(distance)), ... fix(elapsed_time / 3600000), mod(fix(elapsed_time / 60000), 60), ... mod(fix(elapsed_time / 1000), 60), (mod(elapsed_time, 1000))); end |
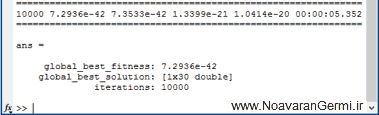
تصویر خروجی 1:
تصویر خروجی 2:

















 (149 امتیاز از 31 رای)
(149 امتیاز از 31 رای)









متشکر که این پروژرو رایگان تو سایت گذاشتین خیلی هم راحت با لینک مستقیم دانلودش کردم .
خیلی خیلی ممنون ، امیدوارم ب کارم بیاد ❤
خوب بود ممنون استفاده کردیم. لطفا الگوریتم های فرا ابتکاری بیشتری رو در سایت بررسی کنید تشکر